T-Formula & Null Hypotheses
Homework #3
9.11
A random sample of size 20 is taken, resulting in a sample mean of 16.45 and a sample standard deviation of 3.59. Assume x is normally distributed and use this information and α = .05 to test the following hypotheses.
H0: µ = 16
Ha: µ ≠ 16
Since both of the following statements is not true with respect to this problem:
- x is normally distributed
- n > 30
We do not use the z-formula; we use the t-formula:
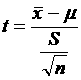
df = n - 1
Decision Rule:
The test is two tailed as Ha uses the not equal assignment.
Confidence level is 1 – α = 1 – .05 = .95
As this is a two-tailed test, there is α/2 or .025 area on each end of the distribution which is the rejection region. Another way to put it is the rejection region covers 2.5% (.025) of each of the two ends of the distribution (total 5%) leaving 95% (.4750) in the non-rejection region.
There is a .4750 area between the mean and each of the critical values that separate the rejection region from the non-rejection region.
From Table A.5 and the .4750 area, the critical z value zα/2 is ±1.96.
Decision Rule:
If the data gathered produces a z value greater than +1.96 or less than -1.96, the decision is to NOT reject the null hypothesis because the observed z value is in the non-rejection region.
Calculate the z value, given:
![]() =
16.45
=
16.45
![]()
n = 20
df = n – 1 = 19
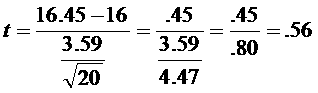
tobserved = .56
For two-tailed tests α/2 = .025, therefore from t-Table Tα/2,df = T.025,19 = ±2.093.
Now, because tobserved (.56) is less than tTable (2.093), we do NOT reject the null hypotheses H0.
